| Section categories |
|
Related Subjects [38]
This category includes brief overview of all related subjects.
|
|
Defining BioInformatics [7]
In this section we tried to briefly explain what bioinformatics is ?
|
|
Unviersities [30]
This contains information about universities that are offering bioinformatics degree programs.
|
|
Resources [24]
Contains information about bioinformatics resources including databases, tools and techniques.
|
|
Algorithms [31]
This category includes some of the basic algorithms that are usually used by bioinformaticians.
|
|
| Statistics |
Total online: 1 Guests: 1 Users: 0 |
|
Home » 2011 » August » 22 » Genetic Algorithms
10:25 PM Genetic Algorithms |
Genetic Algorithms
1. Description: A genetic algorithm (GA) is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems. Genetic algorithms belong to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover.
2. Steps: - Encoding
- Fitness Evaluation
- Reproduction
- Survivor Selection
3. Encoding: - Design alternative à individual (chromosome)
- Single design choice à gene
- Design objectives à fitness
- Example: Problem
- Schedule n jobs on m processors such that the maximum span is minimized.
- Design Alternative: job i ( i=1,2,…n) is assigned to processor j (j=1,2,…,m)
- Individual: A n-vector x such that xi = 1, …,or m
- Design objective: minimize the maximal span
- Fitness: the maximal span for each processor
4. Reproduction: - Reproduction operators
- Crossover
- Two parents produce two offspring
- There is a chance that the chromosomes of the two parents are copied unmodified as offspring
- There is a chance that the chromosomes of the two parents are randomly recombined (crossover) to form offspring
- Generally the chance of crossover is between 0.6 and 1.0
- Mutation
- There is a chance that a gene of a child is changed randomly
- Generally the chance of mutation is low (e.g. 0.001)
5. Reproduction Operators: - Crossover
- Generating offspring from two selected parents
- Single point crossover
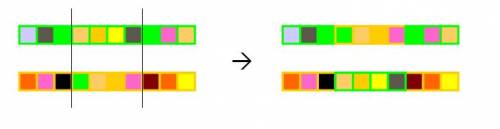
- Two point crossover (Multi point crossover)
- Uniform crossover
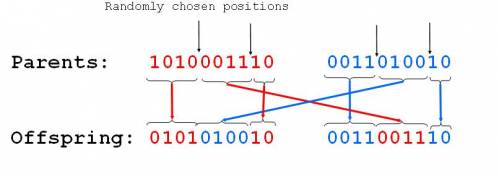
- Randomly one position in the chromosomes is chosen
- Child 1 is head of chromosome of parent 1 with tail of chromosome of parent 2
- Child 2 is head of 2 with tail of 1
- Single point crossover
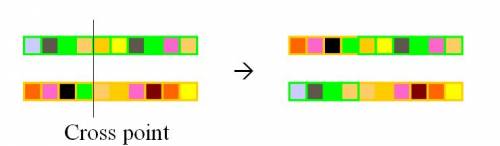 - Two point crossover (Multi point crossover)
 - One-point crossover - Nature
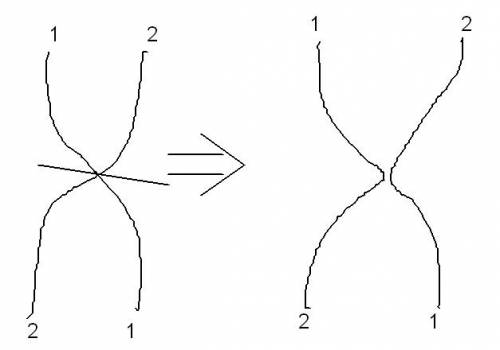 - Two-point crossover
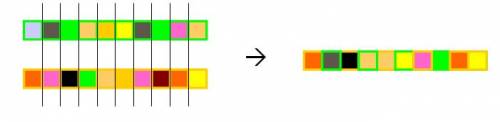
 - Uniform crossover
- A random mask is generated
- The mask determines which bits are copied from one parent and which from the other parent
- Bit density in mask determines how much material is taken from the other parent (takeover parameter)
  - Is uniform crossover better than single crossover point?
- Trade off between
- Exploration: introduction of new combination of features
- Exploitation: keep the good features in the existing solution
- Depending on coding, simple crossovers can have high chance to produce illegal offspring
- E.g. in TSP with simple binary or path coding, most offspring will be illegal because not all cities will be in the offspring and some cities will be there more than once
- Uniform crossover can often be modified to avoid this problem
- E.g. in TSP with simple path coding:
- Where mask is 1, copy cities from one parent
- Where mask is 0, choose the remaining cities in the order of the other parent
- Mutation
- Generating new offspring from single parent
 - Maintaining the diversity of the individuals
- Crossover can only explore the combinations of the current gene pool
- Mutation can "generate” new genes
- Control Parameters: population size, crossover/mutation probability
- Problem specific
- Increase population size
- Increase diversity and computation time for each generation
- Increase crossover probability
- Increase the opportunity for recombination but also disruption of good combination
- Increase mutation probability
- Closer to randomly search
- Help to introduce new gene or reintroduce the lost gene
- Varies The Population:
- Usually using crossover operators to recombine the genes to generate the new population, then using mutation operators on the new population
|
|
|
Category: Algorithms |
Views: 2264 |
Added by: Ansari
| Rating: 0.0/0 |
|
|
|




