The Kabsch algorithm, named after Wolfgang Kabsch, is a method for calculating the optimal rotation matrix that minimizes the RMSD (root mean squared deviation) between two paired sets of points. It is useful in graphics, cheminformatics to compare molecular structures, and also bioinformatics for comparing protein structures.
The algorithm only computes the rotation matrix, but it also requires the computation of a translation vector. When both the translation and rotation are actually performed, the algorithm is sometimes called partial Procrustes superimposition.
2. Description:
The algorithm starts with two sets of paired points, P and Q. Each set of points can be represented as an N×3 matrix. The first row is the coordinates of the first point, the second row is the coordinates of the second point, the Nth row is the coordinates of the Nth point.
The algorithm works in three steps: a translation, the computation of a covariance matrix, and the computation of the optimal rotation matrix.
Translation
Both sets of coordinates must be translated first, so that their centroid coincides with the origin of the coordinate system. This is done by subtracting from the point coordinates the coordinates of the respective centroid.
Computation of the covariance matrix
The second step consist of calculating a covariance matrix A. In matrix notation,
A = PTQ
or, using summation notation,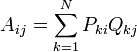
Computation of the optimal rotation matrix
It is possible to calculate the optimal rotation U based on the matrix formula U = (ATA)1 / 2A− 1 but implementing a numerical solution to this formula becomes complicated when all special cases are accounted for (for example, the case of A not having an inverse).
If singular value decomposition (SVD) routines are available, the optimal rotation, U, can be calculated using the following simple algorithm.
First, calculate the SVD of the covariance matrix A.
A = VSWT
Next, decide whether we need to correct our rotation matrix to insure a right-handed coordinate system
d = sign(det(A))
Finally, calculate our optimal rotation matrix, U, as
Generalizations
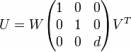
The algorithm was described for points in a three dimensional space. The generalization to D dimensions is immediate.
